Задание №14 ЕГЭ (профильный уровень)
Скачать файл в формате pdf. Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. Прямоугольный параллелепипед, у которого все ребра равны, называется кубом. Если у пирамиды все боковые ребра равны между собой или наклонены под одним и тем же углом к плоскости основания, то основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды эта же точка служит точкой пересечения серединных перпендикуляров к сторонам основания пирамиды. Если у пирамиды боковые грани наклонены к плоскости основания под одним и тем же углом, то основание высоты пирамиды совпадает с центром окружности, вписанной в основание эта же точка служит точкой пересечения биссектрис углов в основании пирамиды.
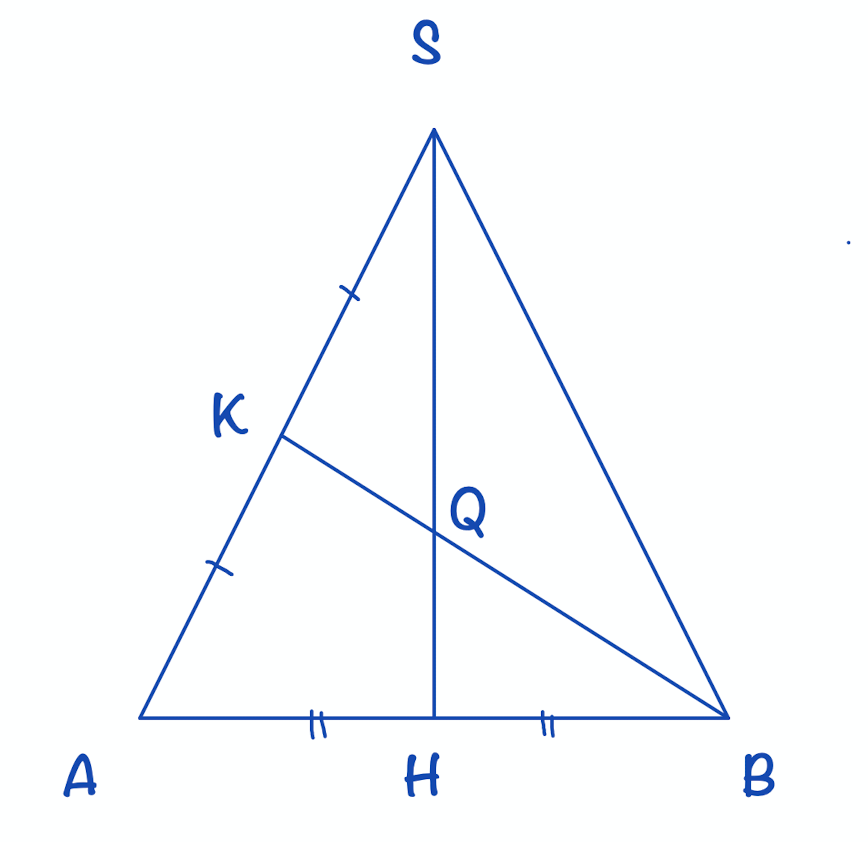
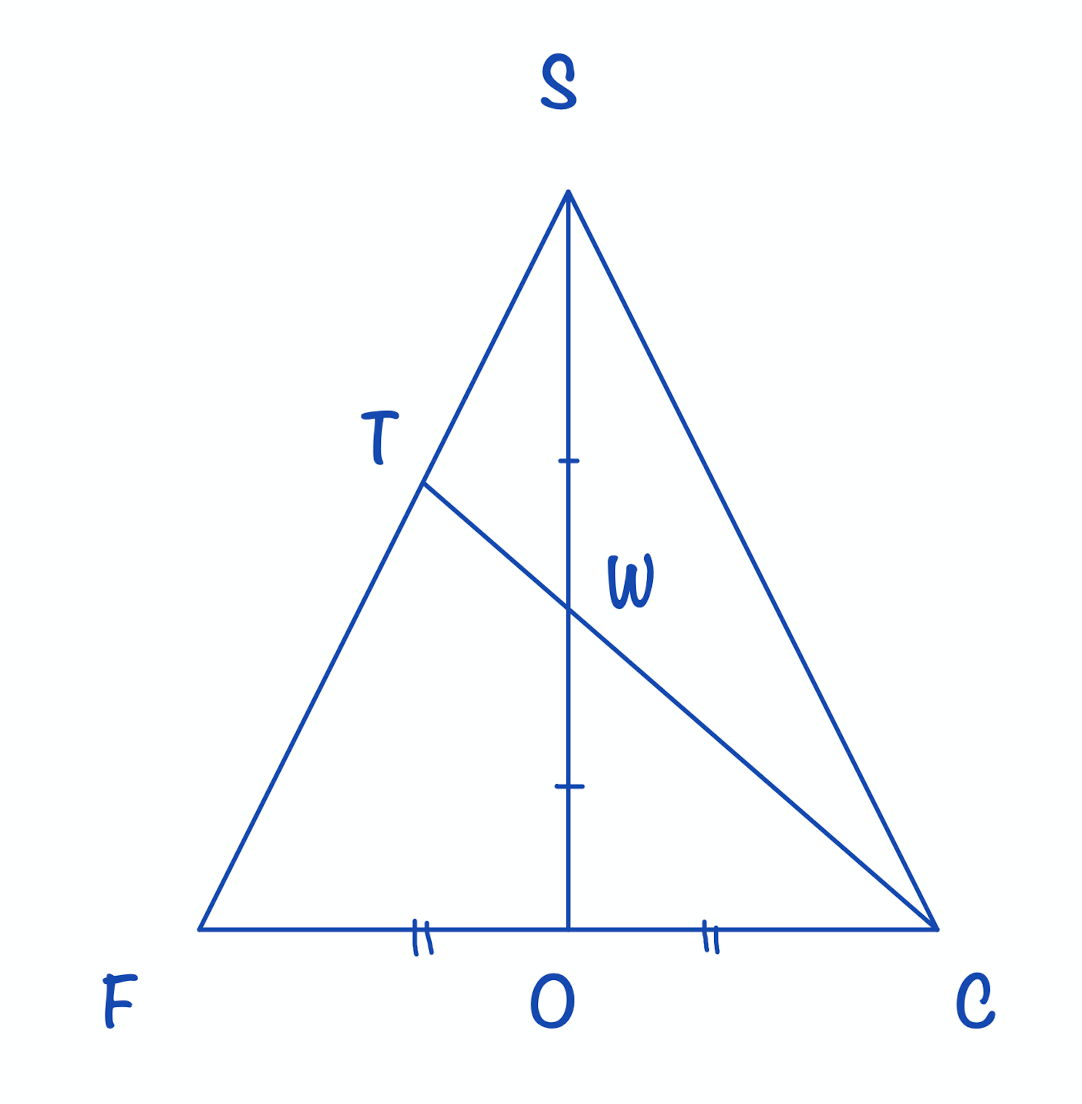








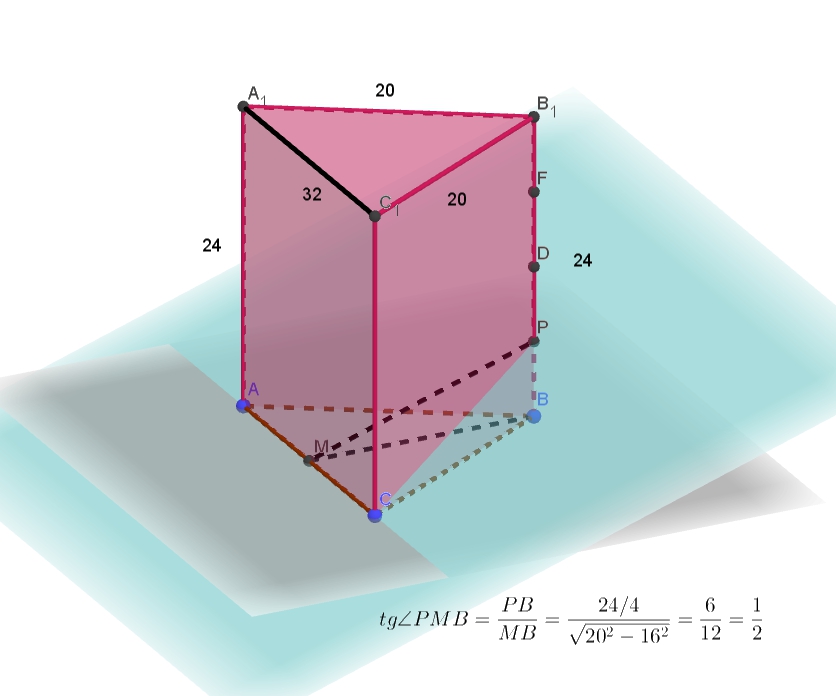
Высота пирамиды проходит через точку В. Через точку А1 перпендикулярно плоскости AB1D1 проведена прямая l. Точка К — середина ребра A1C1. Точка К — середина бокового ребра SD. Продолжая использовать сайт ege








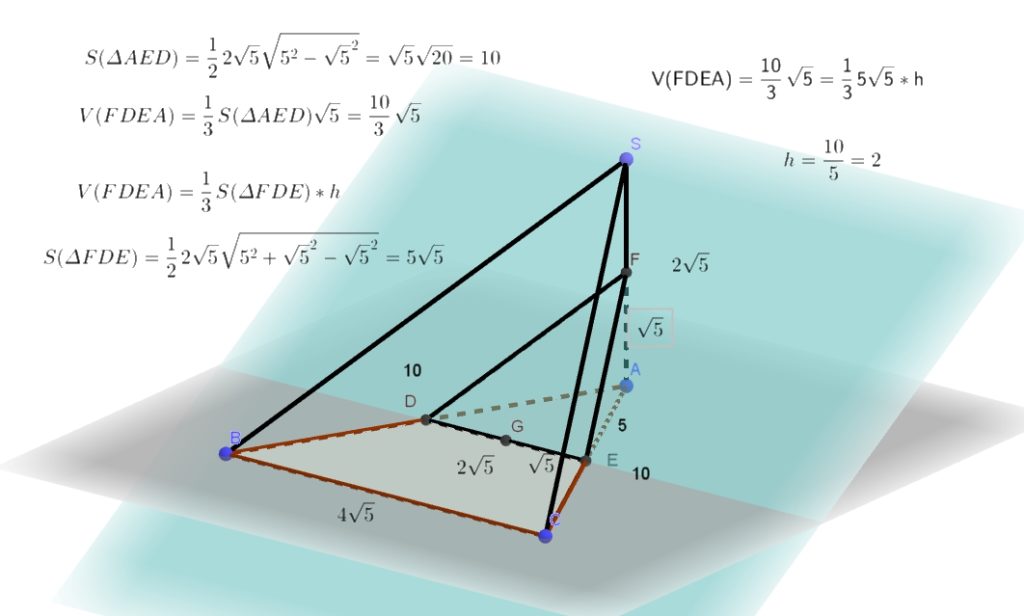
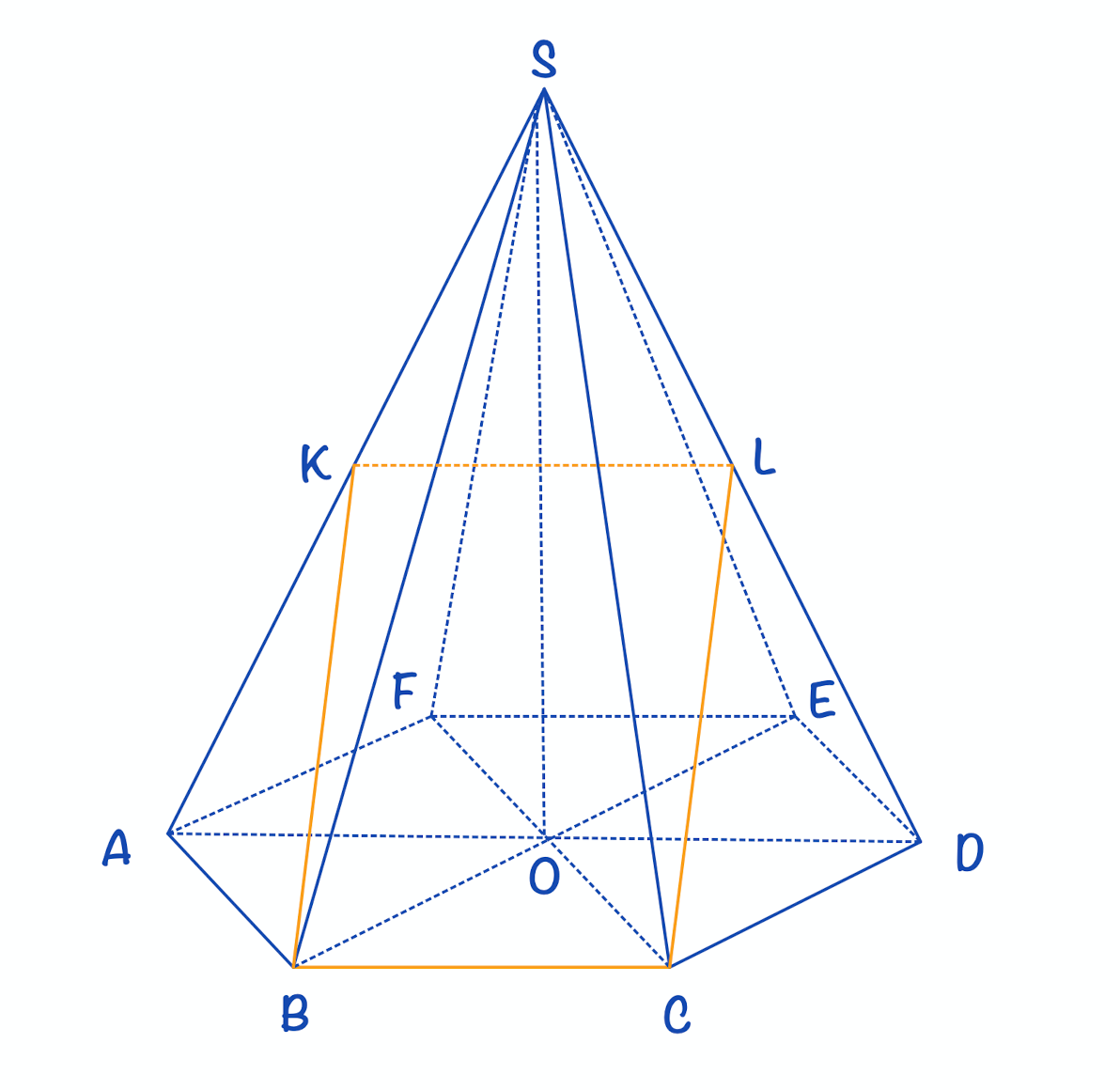

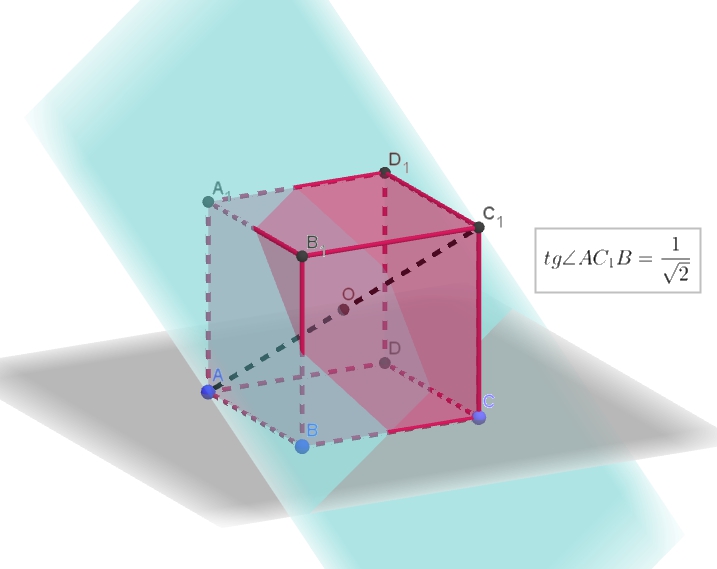
Скачать файл в формате pdf. Угол между плоскостями Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру. Угол между двумя параллельными плоскостями считается равным нулю. Нахождение угла сводится непосредственно к построению и вычислению величины линейного угла двугранного угла, образованного двумя пересекающимися плоскостями. Соответствующий линейный угол строится с помощью двух перпендикуляров, проведенных в указанных плоскостях к прямой их пересечения, а его величина в дальнейшем находится либо из некоторого прямоугольного треугольника, либо из некоторого треугольника с помощью теоремы косинусов. Часто чтобы построить линейный угол между двумя плоскостями находят отрезок перпендикулярный к одной из плоскостей и концы которого лежат в этих плоскостях.